K-means is a popular clustering algorithm that is not only simple, but also very fast and effective, both as a quick hack to preprocess some data and as a production-ready clustering solution. I’ve spent the last few weeks diving deep into GPU programming with CUDA (following this awesome course) and now wanted an interesting real-world algorithm from the field of machine learning to implement using my new GPU programming skills – k-means seemed just right. So in this post, we’ll explore and compare implementations of k-means first in Python, then in C++ (and Eigen) and finally in CUDA.
Mathematical Foundation
Like all good things in machine learning, k-means has a solid mathematical foundation. We’ll want to (briefly) explore its formal definition and express the algorithm in pseudocode before diving into any implementation in a real programming language.
The general framework for k-means defines a set of observations $\mathbf{X} = (\mathbf{x_1}, \mathbf{x_2} , …, \mathbf{x_n})$ consisting of $d$-dimensional points $\mathbf{x_i}$ in some vector space. The goal is to partition this dataset $\mathbf{X}$ into $k$ disjoint subsets $\mathbf{S} = {\mathbb{S_1}, \mathbb{S_2}, …, \mathbb{S_k}}$, such that each point is closer to points inside than outside of its subset. Formally, we are solving the following optimization problem:
\[\text{arg min}_{\mathbf{S}} \sum_{i=1}^k \sum_{\mathbf{x} \in \mathbb{S_i}} ||\mathbf{x} - \mathbf{\mu_i}||^2,\]where $\mu_i$ is the cluster mean or centroid of subset $\mathbb{S_i}$. Since $\sum_x || \mathbf{x} - \mathbf{\mu} ||^2$ also happens to be the variance of $\mathbf{S_i}$, we have an alternative definition given as
\[\text{arg min}_{\mathbf{S}} \sum_{i=1}^k |\mathbf{S_i}| \text{Var}(\mathbf{S_i}),\]which conveys very nicely that we are finding subsets such that the overall variance around cluster centroids is minimized. Note that here I assumed we are measuring distances between points using their Euclidean (or $L_2$) distance, though other distance metrics such as the cosine or manhattan distance would be equally valid.
Now, it turns out that solving this optimization problem is actually NP-hard, so we need some kind of approximation algorithm to solve it in practice. One such approach is called Lloyd’s algorithm, named after Stuart LLoyd who invented it in 1957. This is the one we usually refer to when speaking of k-means (i.e. there is actually not just one k-means algorithm). LLoyd’s algorithm is iterative and decomposes the k-means problem into two distinct, alternating steps: the assignment step and the update step. The full algorithm can be described in pseudocode as follows:
- Given cluster centroids ${\mathbf{\mu_i}}$ initialized in some way,
-
For iteration $t = 1\, ..\, T$:
- Compute the distance from each point $\mathbf{x}$ to each cluster centroid $\mathbf{\mu}$,
- Assign each point to the centroid it is closest to,
- Recompute each centroid $\mathbf{\mu}$ as the mean of all points assigned to it,
where $T$ is the number of iterations we wish to run this algorithm for (typically a few hundred). In each iteration, (1) and (2) are the assignment step and (3) is the update step. The time complexity of this approach is $O(n \times k \times T)$. As you can see, this algorithm is very straightforward and simple. I’d like to emphasize that the first step, cluster initialization, is very important too and bad initialization can delay proper convergence by many iterations. Also, you should notice that steps (1), (2) and to some extent (3) are all highly parallelizable across individual points, which we’ll exploit especially in our CUDA implementations.
One last note I want to make is that k-means is very strongly related to the expectation maximization (EM) algorithm, which maximizes the likelihood of a dataset under some parameterized probability distribution. In fact, k-means is a special case of EM where we assume isotropic (spherical) Gaussian priors.
Python
Let’s begin with the simplest programming language for k-means: Python. The easiest way of implementing k-means in Python is to not do it yourself, but use scipy or scikit-learn instead:
import sklearn.datasets
import sklearn.cluster
import scipy.cluster.vq
import matplotlib.pyplot as plot
n = 100
k = 3
# Generate fake data
data, labels = sklearn.datasets.make_blobs(
n_samples=n, n_features=2, centers=k)
# scipy
means, _ = scipy.cluster.vq.kmeans(data, k, iter=300)
# scikit-learn
kmeans = sklearn.cluster.KMeans(k, max_iter=300)
kmeans.fit(data)
means = kmeans.cluster_centers_
plot.scatter(data[:, 0], data[:, 1], c=labels)
plot.scatter(means[:, 0], means[:, 1], linewidths=2)
plot.show()
Which gives us:
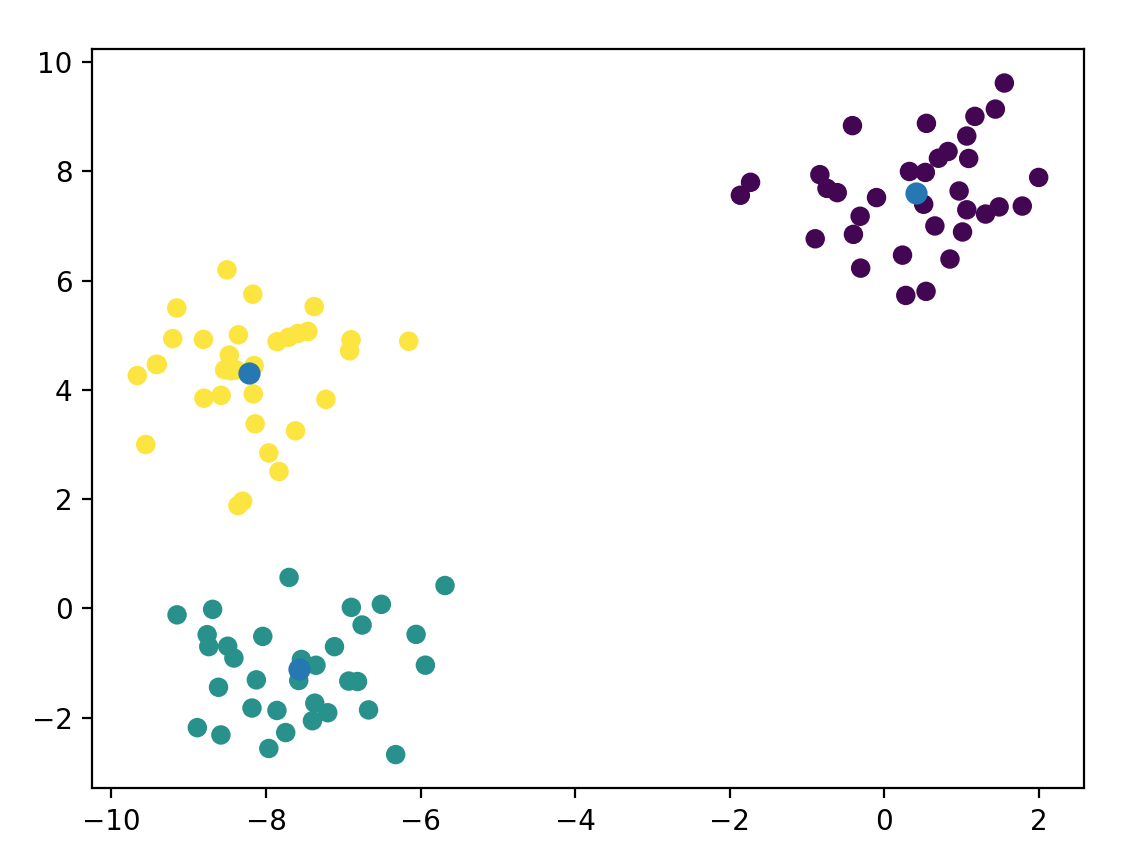
Damn, that was too easy. Definitely not painful enough. Let’s dig deeper and write our own implementation in Python. Before doing so, we need to discuss one aspect that I mentioned above as being important: centroid initialization. That is, what do we set $\mathbf{\mu_i}$ to in the very beginning? A naive idea might be to pick random coordinates within the range ($max - min$) of our data. This turns out to be a very bad idea and leads to slow convergence. A similarly simple but in practice very effective method is to pick random points from our data as the initial centroids. I’ll use this method below. There does exist a superior method called KMeans++ that scikit-learn provides, but we’ll avoid it for simplicity in our code (I will also pick the random-points method when benchmarking scikit-learn).
def k_means(data, k, number_of_iterations):
n = len(data)
number_of_features = data.shape[1]
# Pick random indices for the initial centroids.
initial_indices = np.random.choice(range(n), k)
# We keep the centroids as |features| x k matrix.
means = data[initial_indices].T
# To avoid loops, we repeat the data k times depthwise and compute the
# distance from each point to each centroid in one step in a
# n x |features| x k tensor.
repeated_data = np.stack([data] * k, axis=-1)
all_rows = np.arange(n)
zero = np.zeros([1, 1, 2])
for _ in range(number_of_iterations):
# Broadcast means across the repeated data matrix, gives us a
# n x k matrix of distances.
distances = np.sum(np.square(repeated_data - means), axis=1)
# Find the index of the smallest distance (closest cluster) for each
# point.
assignment = np.argmin(distances, axis=-1)
# Again to avoid a loop, we'll create a sparse matrix with k slots for
# each point and fill exactly the one slot that the point was assigned
# to. Then we reduce across all points to give us the sum of points for
# each cluster.
sparse = np.zeros([n, k, number_of_features])
sparse[all_rows, assignment] = data
# To compute the correct mean, we need to know how many points are
# assigned to each cluster (without a loop).
counts = (sparse != zero).sum(axis=0)
# Compute new assignments.
means = sparse.sum(axis=0).T / counts.clip(min=1).T
return means.T
One thing I want to highlight is that if you plan on writing any kind of reasonably high-performance Python code like here, you’ll want to avoid Python loops at all costs. They will destroy your performance. In my code above, I use a few tricks that allow us to exclusively use NumPy vector operations.
This post is not as much about the k-means algorithm itself as it is about
comparing the performance of implementations of k-means across various
platforms, so we need to know how fast our and scipy/scikit-learn’s
implementation is. Putting simple time.time() calculations immediately around
the function invocations, I get the following results for a dataset of $n \in
{100, 100\,000}$ points, $T = 300$ iterations and $k = 5$ clusters, using the
average time of 5 runs:
| Implementation | $n = 100$ | $n = 100\,000$ |
|---|---|---|
| Our Python | 0.01432s | 7.42498s |
| scikit-learn | 0.00137s | 1.22683s |
| scipy | 0.01474s | 1.54127s |
So, for low numbers our algorithm seems to be fine, but it doesn’t scale well. Scipy and scikit-learn both outsource their computation to C, so they’re simply more efficient.
C++
It seems that pure Python simply cannot keep up with optimized C implementations, so

Spot on Leo, we need to use C++. We’ll begin with a very simple implementation of the algorithm and then see if using the Eigen matrix library can give us any speedup. Here is the code with vanilla C++11/14:
#include <algorithm>
#include <cstdlib>
#include <limits>
#include <random>
#include <vector>
struct Point {
double x{0}, y{0};
};
using DataFrame = std::vector<Point>;
double square(double value) {
return value * value;
}
double squared_l2_distance(Point first, Point second) {
return square(first.x - second.x) + square(first.y - second.y);
}
DataFrame k_means(const DataFrame& data,
size_t k,
size_t number_of_iterations) {
static std::random_device seed;
static std::mt19937 random_number_generator(seed());
std::uniform_int_distribution<size_t> indices(0, data.size() - 1);
// Pick centroids as random points from the dataset.
DataFrame means(k);
for (auto& cluster : means) {
cluster = data[indices(random_number_generator)];
}
std::vector<size_t> assignments(data.size());
for (size_t iteration = 0; iteration < number_of_iterations; ++iteration) {
// Find assignments.
for (size_t point = 0; point < data.size(); ++point) {
double best_distance = std::numeric_limits<double>::max();
size_t best_cluster = 0;
for (size_t cluster = 0; cluster < k; ++cluster) {
const double distance =
squared_l2_distance(data[point], means[cluster]);
if (distance < best_distance) {
best_distance = distance;
best_cluster = cluster;
}
}
assignments[point] = best_cluster;
}
// Sum up and count points for each cluster.
DataFrame new_means(k);
std::vector<size_t> counts(k, 0);
for (size_t point = 0; point < data.size(); ++point) {
const auto cluster = assignments[point];
new_means[cluster].x += data[point].x;
new_means[cluster].y += data[point].y;
counts[cluster] += 1;
}
// Divide sums by counts to get new centroids.
for (size_t cluster = 0; cluster < k; ++cluster) {
// Turn 0/0 into 0/1 to avoid zero division.
const auto count = std::max<size_t>(1, counts[cluster]);
means[cluster].x = new_means[cluster].x / count;
means[cluster].y = new_means[cluster].y / count;
}
}
return means;
}
Let’s see how this super obvious, straight-from-my-brain C++ code fairs for our
100 and 100k data point benchmarks. I compile with -std=c++11 -O3:
| Implementation | $n = 100$ | $n = 100\,000$ |
|---|---|---|
| Our Python | 0.01432s | 7.42498s |
| Our C++ | 0.00054s | 0.26804s |
| scikit-learn | 0.00137s | 1.22683s |
| scipy | 0.01474s | 1.54127s |
Wow, we didn’t even try hard and this C++ implementation is already almost an order of magnitude faster than scikit-learn! Looking at compiler-explorer, we can also see that everything is vectorized beautifully:
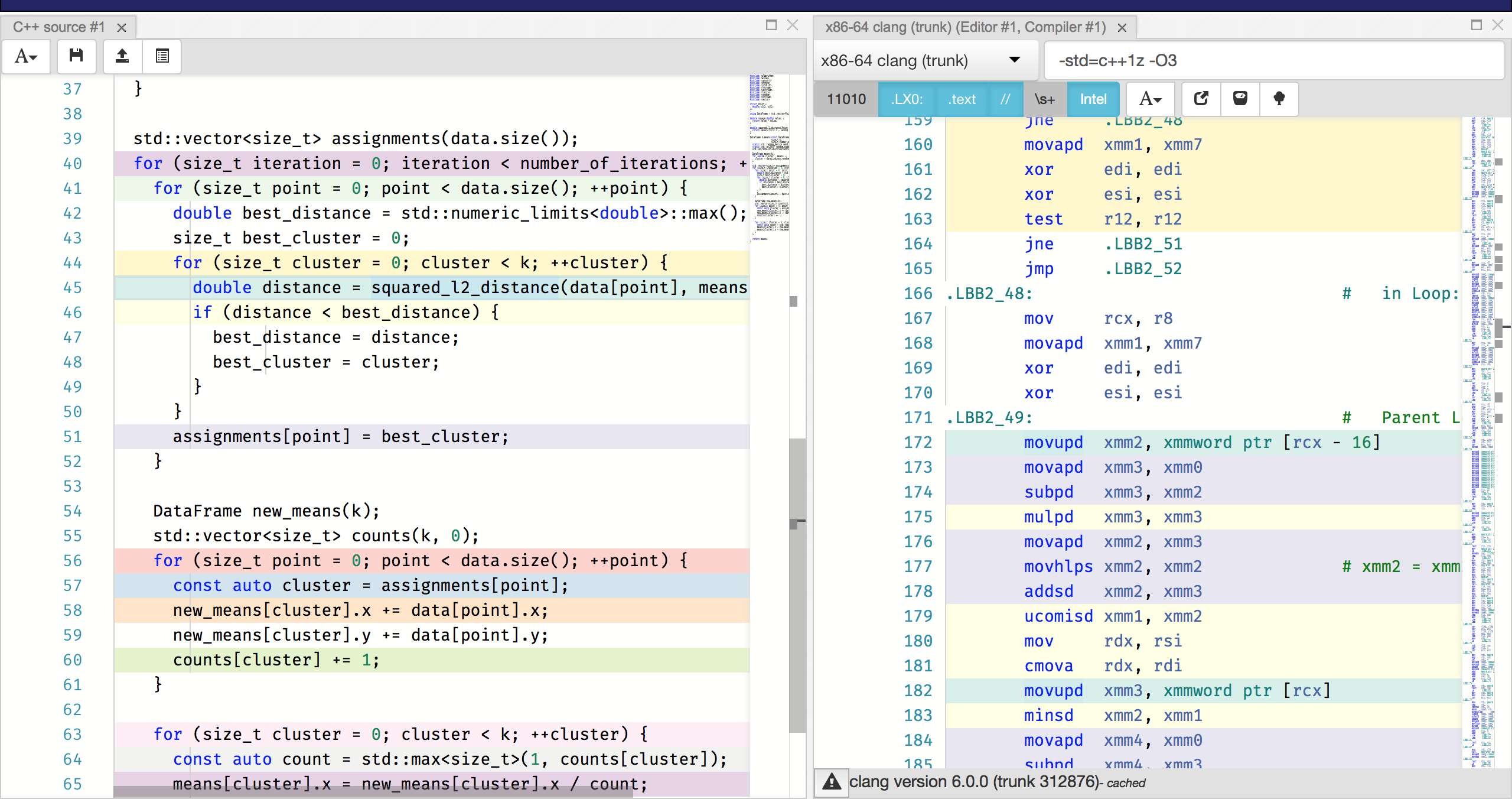
You can see this from the use of xmm registers with packed instructions (ps
or pd suffixes). Thanks, compiler!
Another thing I’ve wanted to try out for a while is Eigen, an apparently fantastic C++ matrix manipulation library underpinning large parts of TensorFlow, for example. Eigen’s power comes from, among many optimizations, its concept of expression templates, which are essentially static computation graphs it can optimize to produce better C++ code under the hood. For example, adding two vectors $\mathbf{a, b}$ together will not immediately perform this operation, but instead result in an object representing this addition. If we then multiply the result with a scalar $s$, for example, Eigen can optimize this whole $s \cdot (\mathbf{a} + \mathbf{b})$ term into a single loop (ideally the compiler should do this for us, but alas, the library helps out).
This was my first time using Eigen and I was hoping it would be like NumPy for Python. It turned out to be that, just in a very limited way. Shortcomings become apparent in its much more simplistic broadcasting functionality and in the fact that tensors (i.e. arrays with rank higher than two) are only experimental, having been introduced by TensorFlow developers but never really integrated with Eigen’s native matrices. So in total I found the experience relatively painful, but I may also have simply been expecting too much coming from NumPy. Anyway, here is my attempt at reproducing my fully vectorized Python code with Eigen:
#include <Eigen/Dense>
#include <cstdlib>
#include <random>
Eigen::ArrayXXd k_means(const Eigen::ArrayXXd &data,
uint16_t k,
size_t number_of_iterations) {
static std::random_device seed;
static std::mt19937 random_number_generator(seed());
std::uniform_int_distribution<size_t> indices(0, data.size() - 1);
Eigen::ArrayX2d means(k, 2);
for (size_t cluster = 0; cluster < k; ++cluster) {
means.row(cluster) = data(indices(random_number_generator));
}
// Because Eigen does not have native tensors, we'll have to split the data by
// features and replicate it across columns to reproduce the approach of
// replicating data across the depth dimension k times.
const Eigen::ArrayXXd data_x = data.col(0).rowwise().replicate(k);
const Eigen::ArrayXXd data_y = data.col(1).rowwise().replicate(k);
for (size_t iteration = 0; iteration < number_of_iterations; ++iteration) {
// This will be optimized nicely by Eigen because it's a large and
// arithmetic-intense expression tree.
Eigen::ArrayXXd distances =
(data_x.rowwise() - means.col(0).transpose()).square() +
(data_y.rowwise() - means.col(1).transpose()).square();
// Unfortunately, Eigen has no vectorized way of retrieving the argmin for
// every row, so we'll have to loop, and iteratively compute the new
// centroids.
Eigen::ArrayX2d sum = Eigen::ArrayX2d::Zero(k, 2);
Eigen::ArrayXd counts = Eigen::ArrayXd::Ones(k);
for (size_t index = 0; index < data.rows(); ++index) {
Eigen::ArrayXd::Index argmin;
distances.row(index).minCoeff(&argmin);
sum.row(argmin) += data.row(index).array();
counts(argmin) += 1;
}
means = sum.colwise() / counts;
}
return means;
}
So, how fast is it?
| Implementation | $n = 100$ | $n = 100\,000$ |
|---|---|---|
| Our Python | 0.01432s | 7.42498s |
| Our C++ | 0.00054s | 0.26804s |
| Our C++ (Eigen) | 0.00055s | 0.56903s |
| scikit-learn | 0.00137s | 1.22683s |
| scipy | 0.01474s | 1.54127s |
The Eigen version of k-means is still a lot faster than scikit-learn, but not quite as fast as the vanilla C++ code. A little disappointing!
CUDA
I mentioned at the very beginning how obviously parallelizable k-means is. Why do I think so? Well, let’s look at the definition of the assignment step:
- Compute the distance from each point $\mathbf{x_i}$ to each cluster centroid $\mathbf{\mu_j}$,
- Assign each point to the centroid it is closest to.
What’s important to notice here is that each data point $\mathbf{x_i}$ does its own thing, i.e. no information or data is shared across individual data points, except for the here immutable cluster centroids. This is nice, because complexity in parallel programming arises almost exclusively when data needs to be shared. If all we’re doing is performing some computation on each point individually, then coding this up on a GPU is a piece of cake.
Things get less rosy when we consider the update step, where we recompute the cluster centroids to be the mean of all points assigned to a particular centroid. Essentially, this is an average reduction, just that we aren’t averaging over all values in the dataset, but doing one reduction over each cluster’s respective subset. The simplest way to do such a reduction is to use an atomic counter. This is slow since the atomic counter increment will be greatly contended and serialize all threads’ accesses. However, it’s easy to implement – so let’s get to it! Here is the CUDA code:
#include <algorithm>
#include <cfloat>
#include <chrono>
#include <random>
#include <vector>
// A small data structure to do RAII for a dataset of 2-dimensional points.
struct Data {
explicit Data(int size) : size(size), bytes(size * sizeof(float)) {
cudaMalloc(&x, bytes);
cudaMalloc(&y, bytes);
}
Data(int size, std::vector<float>& h_x, std::vector<float>& h_y)
: size(size), bytes(size * sizeof(float)) {
cudaMalloc(&x, bytes);
cudaMalloc(&y, bytes);
cudaMemcpy(x, h_x.data(), bytes, cudaMemcpyHostToDevice);
cudaMemcpy(y, h_y.data(), bytes, cudaMemcpyHostToDevice);
}
~Data() {
cudaFree(x);
cudaFree(y);
}
void clear() {
cudaMemset(x, 0, bytes);
cudaMemset(y, 0, bytes);
}
float* x{nullptr};
float* y{nullptr};
int size{0};
int bytes{0};
};
__device__ float
squared_l2_distance(float x_1, float y_1, float x_2, float y_2) {
return (x_1 - x_2) * (x_1 - x_2) + (y_1 - y_2) * (y_1 - y_2);
}
// In the assignment step, each point (thread) computes its distance to each
// cluster centroid and adds its x and y values to the sum of its closest
// centroid, as well as incrementing that centroid's count of assigned points.
__global__ void assign_clusters(const float* __restrict__ data_x,
const float* __restrict__ data_y,
int data_size,
const float* __restrict__ means_x,
const float* __restrict__ means_y,
float* __restrict__ new_sums_x,
float* __restrict__ new_sums_y,
int k,
int* __restrict__ counts) {
const int index = blockIdx.x * blockDim.x + threadIdx.x;
if (index >= data_size) return;
// Make global loads once.
const float x = data_x[index];
const float y = data_y[index];
float best_distance = FLT_MAX;
int best_cluster = 0;
for (int cluster = 0; cluster < k; ++cluster) {
const float distance =
squared_l2_distance(x, y, means_x[cluster], means_y[cluster]);
if (distance < best_distance) {
best_distance = distance;
best_cluster = cluster;
}
}
// Slow but simple.
atomicAdd(&new_sums_x[best_cluster], x);
atomicAdd(&new_sums_y[best_cluster], y);
atomicAdd(&counts[best_cluster], 1);
}
// Each thread is one cluster, which just recomputes its coordinates as the mean
// of all points assigned to it.
__global__ void compute_new_means(float* __restrict__ means_x,
float* __restrict__ means_y,
const float* __restrict__ new_sum_x,
const float* __restrict__ new_sum_y,
const int* __restrict__ counts) {
const int cluster = threadIdx.x;
// Threshold count to turn 0/0 into 0/1.
const int count = max(1, counts[cluster]);
means_x[cluster] = new_sum_x[cluster] / count;
means_y[cluster] = new_sum_y[cluster] / count;
}
int main(int argc, const char* argv[]) {
std::vector<float> h_x;
std::vector<float> h_y;
// Load x and y into host vectors ... (omitted)
const size_t number_of_elements = h_x.size();
Data d_data(number_of_elements, h_x, h_y);
// Random shuffle the data and pick the first
// k points (i.e. k random points).
std::random_device seed;
std::mt19937 rng(seed());
std::shuffle(h_x.begin(), h_x.end(), rng);
std::shuffle(h_y.begin(), h_y.end(), rng);
Data d_means(k, h_x, h_y);
Data d_sums(k);
int* d_counts;
cudaMalloc(&d_counts, k * sizeof(int));
cudaMemset(d_counts, 0, k * sizeof(int));
const int threads = 1024;
const int blocks = (number_of_elements + threads - 1) / threads;
for (size_t iteration = 0; iteration < number_of_iterations; ++iteration) {
cudaMemset(d_counts, 0, k * sizeof(int));
d_sums.clear();
assign_clusters<<<blocks, threads>>>(d_data.x,
d_data.y,
d_data.size,
d_means.x,
d_means.y,
d_sums.x,
d_sums.y,
k,
d_counts);
cudaDeviceSynchronize();
compute_new_means<<<1, k>>>(d_means.x,
d_means.y,
d_sums.x,
d_sums.y,
d_counts);
cudaDeviceSynchronize();
}
}
This is largely unoptimized CUDA code that makes no effort to come up with an
efficient parallel algorithm to perform the reduction (we’ll get to one in a
bit). I’ll compile this with nvcc -std=c++11 -O3 and run on a fairly recent
NVIDIA Titan X (PASCAL) GPU. And?
| Implementation | $n = 100$ | $n = 100\,000$ |
|---|---|---|
| Our Python | 0.01432s | 7.42498s |
| Our C++ | 0.00054s | 0.26804s |
| Our C++ (Eigen) | 0.00055s | 0.56903s |
| Our CUDA | 0.00956s | 0.0752s |
| scikit-learn | 0.00137s | 1.22683s |
| scipy | 0.01474s | 1.54127s |
Interesting! Running a GPU for 100 data points is a little like launching a space rocket to get from the living room to the kitchen in your house: totally unnecessary, not using the full potential of the vehicle and the overhead of launching itself will outweigh any benefits once the rocket, or GPU kernel, is running. On the other hand, we see that GPUs simply scale so beautifully across data when looking at the 100k experiment. Whereas the assignment step in our previous CPU algorithm scaled linearly w.r.t. the number of observations in our dataset, the span complexity of our GPU implementation stays constant and only the overall work increases. That is, adding more data does not alter the overall execution time (in theory). Of course, this only holds if you have enough threads to assign one to each point. In my experiments here I will assume such favorable circumstances.
As part of my exploration of GPU programming, I also wanted to try out Thrust, a cool library that provides STL-like abstractions and containers while encapsulating the nasty memory management I did manually above. The same code above, in Thrust, is a little shorter:
#include <thrust/device_vector.h>
#include <thrust/host_vector.h>
__device__ float
squared_l2_distance(float x_1, float y_1, float x_2, float y_2) {
return (x_1 - x_2) * (x_1 - x_2) + (y_1 - y_2) * (y_1 - y_2);
}
// In the assignment step, each point (thread) computes its distance to each
// cluster centroid and adds its x and y values to the sum of its closest
// centroid, as well as incrementing that centroid's count of assigned points.
__global__ void assign_clusters(const thrust::device_ptr<float> data_x,
const thrust::device_ptr<float> data_y,
int data_size,
const thrust::device_ptr<float> means_x,
const thrust::device_ptr<float> means_y,
thrust::device_ptr<float> new_sums_x,
thrust::device_ptr<float> new_sums_y,
int k,
thrust::device_ptr<int> counts) {
const int index = blockIdx.x * blockDim.x + threadIdx.x;
if (index >= data_size) return;
// Make global loads once.
const float x = data_x[index];
const float y = data_y[index];
float best_distance = FLT_MAX;
int best_cluster = 0;
for (int cluster = 0; cluster < k; ++cluster) {
const float distance =
squared_l2_distance(x, y, means_x[cluster], means_y[cluster]);
if (distance < best_distance) {
best_distance = distance;
best_cluster = cluster;
}
}
atomicAdd(thrust::raw_pointer_cast(new_sums_x + best_cluster), x);
atomicAdd(thrust::raw_pointer_cast(new_sums_y + best_cluster), y);
atomicAdd(thrust::raw_pointer_cast(counts + best_cluster), 1);
}
// Each thread is one cluster, which just recomputes its coordinates as the mean
// of all points assigned to it.
__global__ void compute_new_means(thrust::device_ptr<float> means_x,
thrust::device_ptr<float> means_y,
const thrust::device_ptr<float> new_sum_x,
const thrust::device_ptr<float> new_sum_y,
const thrust::device_ptr<int> counts) {
const int cluster = threadIdx.x;
const int count = max(1, counts[cluster]);
means_x[cluster] = new_sum_x[cluster] / count;
means_y[cluster] = new_sum_y[cluster] / count;
}
int main(int argc, const char* argv[]) {
thrust::host_vector<float> h_x;
thrust::host_vector<float> h_y;
// Load x and y into host vectors ... (omitted)
const size_t number_of_elements = h_x.size();
thrust::device_vector<float> d_x = h_x;
thrust::device_vector<float> d_y = h_y;
std::mt19937 rng(std::random_device{}());
std::shuffle(h_x.begin(), h_x.end(), rng);
std::shuffle(h_y.begin(), h_y.end(), rng);
thrust::device_vector<float> d_mean_x(h_x.begin(), h_x.begin() + k);
thrust::device_vector<float> d_mean_y(h_y.begin(), h_y.begin() + k);
thrust::device_vector<float> d_sums_x(k);
thrust::device_vector<float> d_sums_y(k);
thrust::device_vector<int> d_counts(k, 0);
const int threads = 1024;
const int blocks = (number_of_elements + threads - 1) / threads;
for (size_t iteration = 0; iteration < number_of_iterations; ++iteration) {
thrust::fill(d_sums_x.begin(), d_sums_x.end(), 0);
thrust::fill(d_sums_y.begin(), d_sums_y.end(), 0);
thrust::fill(d_counts.begin(), d_counts.end(), 0);
assign_clusters<<<blocks, threads>>>(d_x.data(),
d_y.data(),
number_of_elements,
d_mean_x.data(),
d_mean_y.data(),
d_sums_x.data(),
d_sums_y.data(),
k,
d_counts.data());
cudaDeviceSynchronize();
compute_new_means<<<1, k>>>(d_mean_x.data(),
d_mean_y.data(),
d_sums_x.data(),
d_sums_y.data(),
d_counts.data());
cudaDeviceSynchronize();
}
}
The running time of this code is actually slightly lower for the 100 point
version, but equal to the pure CUDA version for 100k points. I don’t really
consider Thrust to be a separate platform or algorithm, so I won’t list it in
the comparison. This more to see what working with Thrust is like (not doing
manual cudaMalloc is nice).
Now, even though we can be quite happy with this speedup already, we haven’t really invested much effort into this. Using atomic operations is somewhat cheating and definitely does not use the full capacity of GPUs, since the 100,000 threads we launch ultimately have to queue up behind each other to make their increments. Also, there is one particularly awful line in the above code that makes the implementation slow and that is somewhat easy to fix, without requiring deep algorithmic changes. It’s this one here:
const float distance =
squared_l2_distance(x, y, means_x[cluster], means_y[cluster]);
I’m not talking about the function call, but about the global memory loads
means_x[cluster] and means_y[cluster]. Having every thread go to global
memory to fetch the cluster means is inefficient. One of the first things we
learn about GPU programming is that understanding and utilizing the memory
hierarchy in GPUs is essential to building efficient programs, much more so than
on CPUs, where compilers or the hardware itself handle register allocation and
caching for us. The simple fix for the above global memory loads is to place the
means into shared memory and have the threads load them from there. The code
changes are quite minor. First in the assign_clusters kernel:
__global__ void assign_clusters(const float* __restrict__ data_x,
const float* __restrict__ data_y,
int data_size,
const float* __restrict__ means_x,
const float* __restrict__ means_y,
float* __restrict__ new_sums_x,
float* __restrict__ new_sums_y,
int k,
int* __restrict__ counts) {
// We'll copy means_x and means_y into shared memory.
extern __shared__ float shared_means[];
const int index = blockIdx.x * blockDim.x + threadIdx.x;
if (index >= data_size) return;
// Let the first k threads copy over the cluster means.
if (threadIdx.x < k) {
// Using a flat array where the first k entries are x and the last k are y.
shared_means[threadIdx.x] = means_x[threadIdx.x];
shared_means[k + threadIdx.x] = means_y[threadIdx.x];
}
// Wait for those k threads.
__syncthreads();
// Make global loads once.
const float x = data_x[index];
const float y = data_y[index];
float best_distance = FLT_MAX;
int best_cluster = 0;
for (int cluster = 0; cluster < k; ++cluster) {
// Neatly access shared memory.
const float distance = squared_l2_distance(x,
y,
shared_means[cluster],
shared_means[k + cluster]);
if (distance < best_distance) {
best_distance = distance;
best_cluster = cluster;
}
}
atomicAdd(&new_sums_x[best_cluster], x);
atomicAdd(&new_sums_y[best_cluster], y);
atomicAdd(&counts[best_cluster], 1);
}
Then in the kernel launch:
int main(int argc, const char* argv[]) {
const int threads = 1024;
const int blocks = (number_of_elements + threads - 1) / threads;
const int shared_memory = d_means.bytes * 2;
// ...
for (size_t iteration = 0; iteration < number_of_iterations; ++iteration) {
assign_clusters<<<blocks, threads, shared_memory>>>(d_data.x,
d_data.y,
d_data.size,
d_means.x,
d_means.y,
d_sums.x,
d_sums.y,
k,
d_counts);
// ...
}
}
Easy. Is the improvement noticeable? Let’s see:
| Implementation | $n = 100$ | $n = 100\,000$ |
|---|---|---|
| Our Python | 0.01432s | 7.42498s |
| Our C++ | 0.00054s | 0.26804s |
| Our C++ (Eigen) | 0.00055s | 0.56903s |
| Our CUDA | 0.00956s | 0.0752s |
| Our CUDA (2) | 0.00878s | 0.0611s |
| scikit-learn | 0.00137s | 1.22683s |
| scipy | 0.01474s | 1.54127s |
Indeed, sweet! But we’re still doing atomic increments, so let’s think a bit more.
Serial reductions like the averaging operation we are performing during the update step scale linearly (we need to touch each observation once). However, parallel reductions can be implemented efficiently with only $\log n$ steps using a tree-reduction. You can read more about this here. Conceptually, you can think of a tree-reduction like this:
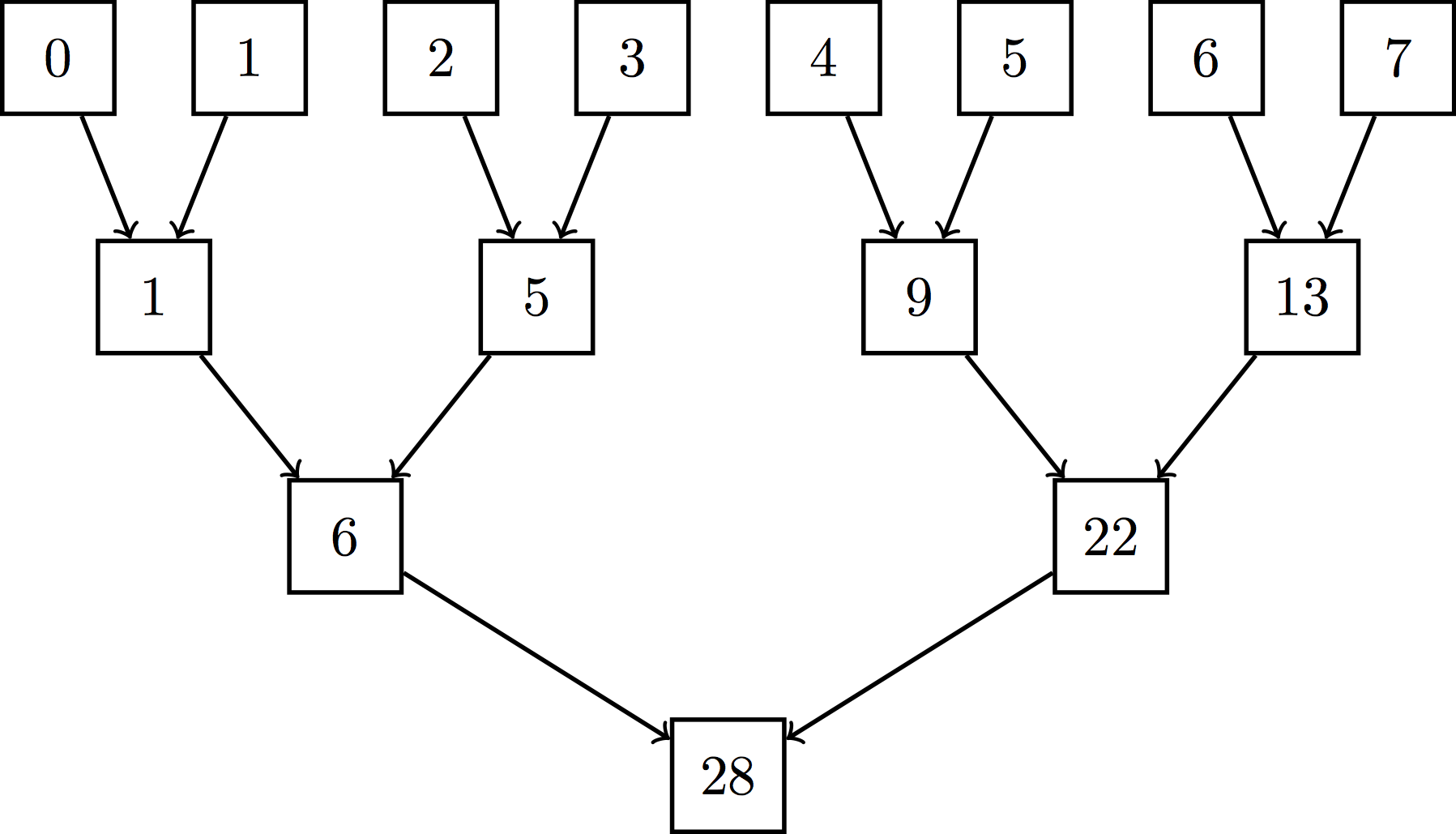
though practically speaking, we implement it more like so:
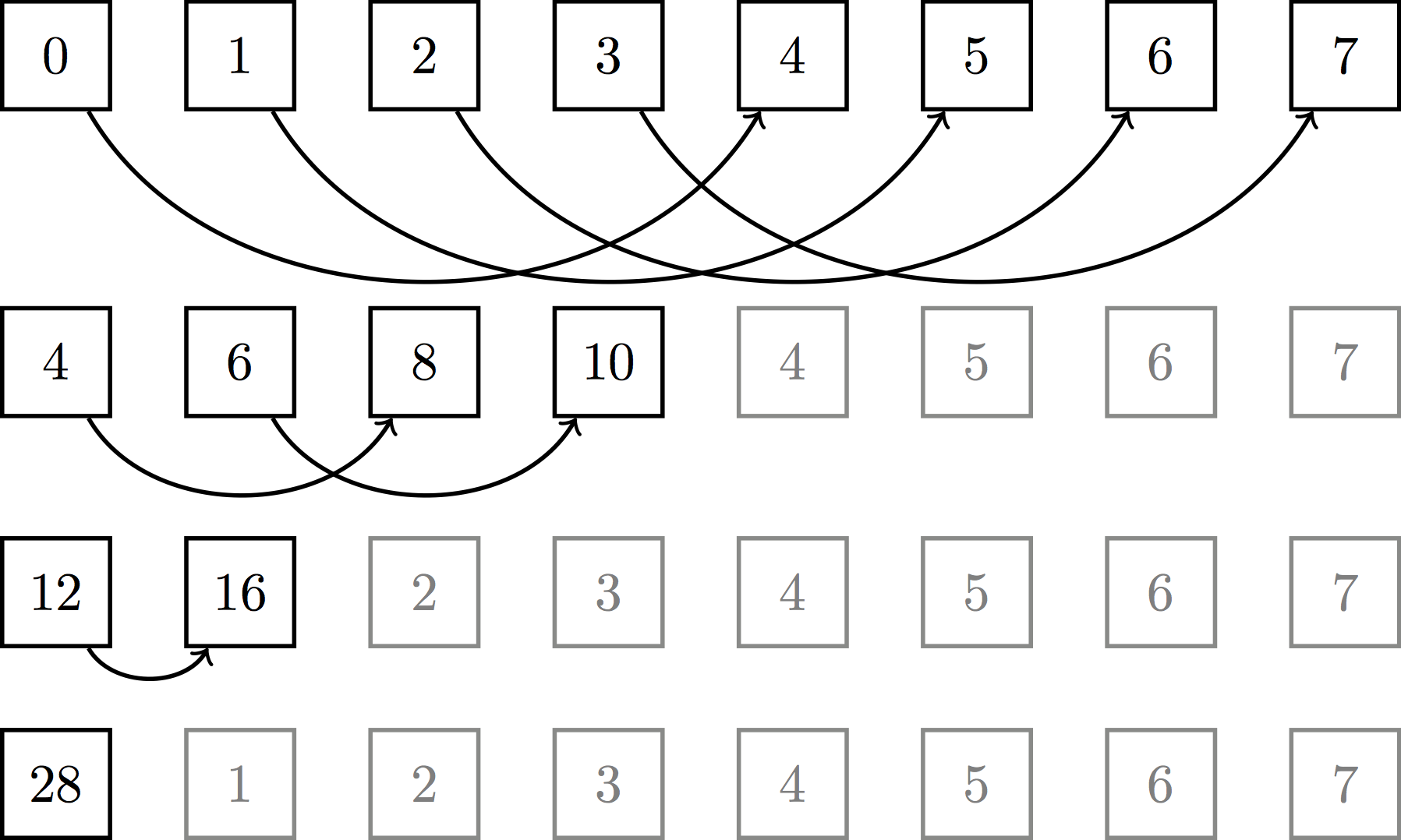
The work complexity is still the same ($n - 1$ addition operations), but the span complexity is only logarithmic. For large $n$, this benefit is enormous. One thing to note about the practical implementation of this tree reduction is that it requires two kernel launches. The first performs block-wise reductions, yielding the sum of all values for each block. The second then launches one more thread block to reduce those block-wise sums into a single, overall sum (this assumes we have enough threads and stuff).
Now, the tricky thing in our case is that we can’t just average over all our data. Instead, for each cluster, we have to only average over the points assigned to that cluster. There’s a few ways we could solve this problem. One idea would be to sort the data by their assignment, so that points in the same cluster are next to each other in memory, then do one standard reduction per segment.
The approach I picked is a bit different. Essentially, I wanted to do more work in the same kernel. So my idea was the following: keep a shared memory segment in each thread block and for each cluster and each thread, check if the thread is assigned to the cluster and write the thread’s value into the shared memory segment if yes, otherwise write a zero in that place. Then do a simple reduction. Since we also need the count of assigned points per cluster, we can also map values to zeros and ones and reduce over those in the same sweep to get the cluster counts. This approach has both very high shared memory utilization and overall occupancy (we’re doing lots of work in each block and in many blocks). Here is the code for the “fine”, per-block reduction (it’s quite a lot):
__global__ void fine_reduce(const float* __restrict__ data_x,
const float* __restrict__ data_y,
int data_size,
const float* __restrict__ means_x,
const float* __restrict__ means_y,
float* __restrict__ new_sums_x,
float* __restrict__ new_sums_y,
int k,
int* __restrict__ counts) {
// Essentially three dimensional: n * x, n * y, n * counts.
extern __shared__ float shared_data[];
const int local_index = threadIdx.x;
const int global_index = blockIdx.x * blockDim.x + threadIdx.x;
if (global_index >= data_size) return;
// Load the mean values into shared memory.
if (local_index < k) {
shared_data[local_index] = means_x[local_index];
shared_data[k + local_index] = means_y[local_index];
}
__syncthreads();
// Assignment step.
// Load once here.
const float x_value = data_x[global_index];
const float y_value = data_y[global_index];
float best_distance = FLT_MAX;
int best_cluster = -1;
for (int cluster = 0; cluster < k; ++cluster) {
const float distance = squared_l2_distance(x_value,
y_value,
shared_data[cluster],
shared_data[k + cluster]);
if (distance < best_distance) {
best_distance = distance;
best_cluster = cluster;
}
}
__syncthreads();
// Reduction step.
const int x = local_index;
const int y = local_index + blockDim.x;
const int count = local_index + blockDim.x + blockDim.x;
for (int cluster = 0; cluster < k; ++cluster) {
// Zeros if this point (thread) is not assigned to the cluster, else the
// values of the point.
shared_data[x] = (best_cluster == cluster) ? x_value : 0;
shared_data[y] = (best_cluster == cluster) ? y_value : 0;
shared_data[count] = (best_cluster == cluster) ? 1 : 0;
__syncthreads();
// Tree-reduction for this cluster.
for (int stride = blockDim.x / 2; stride > 0; stride /= 2) {
if (local_index < stride) {
shared_data[x] += shared_data[x + stride];
shared_data[y] += shared_data[y + stride];
shared_data[count] += shared_data[count + stride];
}
__syncthreads();
}
// Now shared_data[0] holds the sum for x.
if (local_index == 0) {
const int cluster_index = blockIdx.x * k + cluster;
new_sums_x[cluster_index] = shared_data[x];
new_sums_y[cluster_index] = shared_data[y];
counts[cluster_index] = shared_data[count];
}
__syncthreads();
}
}
Note that we perform the assignment and block-wise reduction in the same kernel. Then, we do a coarse reduction to sum the block-wise values into a final, single value:
__global__ void coarse_reduce(float* __restrict__ means_x,
float* __restrict__ means_y,
float* __restrict__ new_sum_x,
float* __restrict__ new_sum_y,
int k,
int* __restrict__ counts) {
extern __shared__ float shared_data[];
const int index = threadIdx.x;
const int y_offset = blockDim.x;
// Load into shared memory for more efficient reduction.
shared_data[index] = new_sum_x[index];
shared_data[y_offset + index] = new_sum_y[index];
__syncthreads();
for (int stride = blockDim.x / 2; stride >= k; stride /= 2) {
if (index < stride) {
shared_data[index] += shared_data[index + stride];
shared_data[y_offset + index] += shared_data[y_offset + index + stride];
}
__syncthreads();
}
// The first k threads can recompute their clusters' means now.
if (index < k) {
const int count = max(1, counts[index]);
means_x[index] = new_sum_x[index] / count;
means_y[index] = new_sum_y[index] / count;
new_sum_y[index] = 0;
new_sum_x[index] = 0;
counts[index] = 0;
}
}
Recall that in the fine reduction step, each block produces one sum per cluster. As such, you can visualize the input to the coarse reduction like this:

The goal is to combine all these values into $k$ sums, by summing up the individual, block-wise cluster sums (i.e. have one sum for each $k_i$). To do so, we simply stop the reduction at stride $k$, as you can see in the code above. Easy.
The last step is to launch the kernels of course:
// * 3 for x, y and counts.
const int fine_shared_memory = 3 * threads * sizeof(float);
// * 2 for x and y. Will have k * blocks threads for the coarse reduction.
const int coarse_shared_memory = 2 * k * blocks * sizeof(float);
// ...
for (size_t iteration = 0; iteration < number_of_iterations; ++iteration) {
fine_reduce<<<blocks, threads, fine_shared_memory>>>(d_data.x,
d_data.y,
d_data.size,
d_means.x,
d_means.y,
d_sums.x,
d_sums.y,
k,
d_counts);
cudaDeviceSynchronize();
coarse_reduce<<<1, k * blocks, coarse_shared_memory>>>(d_means.x,
d_means.y,
d_sums.x,
d_sums.y,
k,
d_counts);
cudaDeviceSynchronize();
}
With all this effort and algorithmic stuff, we’d hope to have some gains from this, right? (Or if not, we’d call it a commendable scientific effort). Let’s see:
| Implementation | $n = 100$ | $n = 100\,000$ |
|---|---|---|
| Our Python | 0.01432s | 7.42498s |
| Our C++ | 0.00054s | 0.26804s |
| Our C++ (Eigen) | 0.00055s | 0.56903s |
| Our CUDA | 0.00956s | 0.0752s |
| Our CUDA (2) | 0.00878s | 0.0611s |
| Our CUDA (3) | 0.00822s | 0.0171s |
| scikit-learn | 0.00137s | 1.22683s |
| scipy | 0.01474s | 1.54127s |
Boom, that’s fast! Our CUDA implementation is around 72 times faster than scikit-learn and 90 times faster than scipy (for large data). That’s pretty neat. It’s also nearly 16 times faster than plain C++.
Conclusion
So is this the best we can do? Definitely not. I imagine someone with more GPU
programming experience could get even more out of it. nvprof does give me
pretty good specs, but I’m certain that the right intrinsics and loop unrolling
tricks sprinkled around could speed up the implementation even more. If you have
any ideas, let me know! I’ve published all my code in this
repository.
In conclusion, I have to say that GPU programming with CUDA is a lot of fun. I’ve realized that dealing with such highly parallel code and hundreds of thousands of threads requires a whole new set of techniques. Even simple reductions like the ones we used here have to be approached completely differently than on serial CPUs. But getting speedups like the ones we saw is definitely amazing. I feel like I’ve gained a much greater appreciation for the algorithms that make my neural networks run 10x faster on a single GPU than even on a 32-core CPU. But there’s so much more to explore in this space. Apparently convolutions are supposed to be pretty fast on GPUs?
